Álgebra, Geometría y Estadistica
- Manuela Agudelo Agudelo, Milena Martinez Carmona
- 11 nov 2015
- 13 Min. de lectura
Estadistica:
Numeros reales y expresiones algebraicas:
*Numeros reales:
En matemáticas,el conjunto de los números reales (denotado por ℝ) incluye tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.
Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
Conjuntos numéricos:
Los números naturales:
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
La suma y el producto de dos números naturales es otro número natural.
La diferencia de dos números naturales no siempre es un número natural, sólo ocurre cuando el minuendo es mayor que sustraendo.
5 − 3
3 − 5
El cociente de dos números naturales no siempre es un número natural, sólo ocurre cuando la división es exacta.
6 : 2
2 : 6
Podemos utilizar potencias, ya que es la forma abreviada de escribir un producto formado por varios factores iguales.
La raíz de un número natural no siempre es un número natural, sólo ocurre cuando la raíz es exacta.
Los números enteros
Los números enteros son del tipo:
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
La suma, la diferencia y el producto de dos números enteros es otro número entero.
El cociente de dos números enteros no siempre es un número entero , sólo ocurre cuando la división es exacta.
6 : 2
2 : 6
Podemos operar con potencias, pero el exponente tiene que ser un número natural.
La raíz de un número entero no siempre es un número entero, sólo ocurre cuando la raíz es exacta o si se trata de una raíz de índice par con radicando positivo.
Los números racionales:
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.
Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.
La suma, la diferencia , el producto y el cociente de dos números racionales es otro número racional.
Podemos operar con potencias, pero el exponente tiene que ser un número entero.
La raíz de un número racional no siempre es un número racional, sólo ocurre cuando la raíz es exacta y si el índice es par el radicando ha de ser positivo.
Los números irracionales:
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es , que se define como la relación entre la longitud de la circunferencia y su diámetro.
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo, , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
Los números reales:
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por .
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
La recta real:
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
expresiones algebraicas:
consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.
Las expresiones algebraicas nos permiten, por ejemplo, hallar áreas y volúmenes.
Longitud de la circunferencia: 2πr, donde r es el radio de la circunferencia.
Área del cuadrado: S = l2, donde l es el lado del cuadrado.
Volumen del cubo: V = a3, donde a es la arista del cubo.
Expresiones algebraicas comunes:
El doble o duplo de un número: 2x
El triple de un número: 3x
El cuádruplo de un número: 4x
La mitad de un número: x/2
Un tercio de un número: x/3
Un cuarto de un número: x/4
Un número es proporcional a 2, 3, 4...: 2x, 3x, 4x...
Un número al cuadrado: x²
Un número al cubo: x³
Un número par: 2x
Un número impar: 2x + 1
Dos números consecutivos: x y x + 1
Dos números consecutivos pares: 2x y 2x + 2
Dos números consecutivos impares: 2x + 1 y 2x + 3
Descomponer 24 en dos partes: x y 24 − x
La suma de dos números es 24: x y 24 − x
La diferencia de dos números es 24: x y 24 + x
El producto de dos números es 24: x y 24/x
El cociente de dos números es 24: x y 24 · x
La adiccion en las expresiones algebraicas:
Leyes:
1. Cuando se suman términos semejantes con el mismo signo, los coeficientes se suman y mantienen el mismo signo. Es decir:
(+) + (+) = +
(–) + (–) = –
2.Cuando se suman términos semejantes con signos diferentes, los coeficientes se restan y se le pone el signo de la cantidad de mayor valor absoluto. Es decir,
(–) + (+) = El signo del número mayor
(+) + (–) = El signo del número mayor
Simbolos de agrupacion:
En la suma de dos o más cantidades no cambia de valor si se suprimen los símbolos de agrupación: “( ), [ ], { }”; ejemplos: (+ a) + (+ b) + (+ c) = a + b + c (- a) + (- b) + (- c) = - a - b - c (a) + (+ b) + (- c) = a + b - c (a + b) + (c + d) = a + b + c + d (-a -b) + (-c -d) = - a – b – c – d (a –b) + (c – d)= a – b + c – d Para sumar o restar términos algebraicos deben ser términos semejantes, es decir, que tengan las mismas literales afectadas por los mismos exponentes. También se puede decir, que es una reducción de términos semejantes. Se pueden presentar los siguientes casos:
Primer caso:
Suma de monomios De acuerdo a las leyes de los signos, se tiene que:
*2x2y3z + 3x2y3z = (2 + 3)x2y3z = 5x2y3z
Segundo Caso:
Suma de polinomios Para sumar polinomios. Se colocan los términos semejantes unos debajo de otros; y, se hace la reducción de los términos semejantes, teniendo en cuenta las leyes de los signos.
*P(x) = 7x4 + 4x2 + 7x + 2
Q(x) = 6x3 + 8x +3
Se agrupan unos debajo del otro segun su variable
NOTAS:
Para sumar términos semejantes basta sumar los coeficientes y escribir a continuación la literal o literales Para sumar términos que no son semejantes se deja indicada la operación. Para sumar términos semejantes con otros que no lo son se suman los términos semejantes y los demás se escriben a continuación En álgebra se emplean los mismos signos que en aritmética, y con el mismo significado Cuando una cantidad no tiene escrito su signo se toma como positiva.
La resta en las expresiones algebraicas:
La resta o sustracción es la operación contraria de la suma. Restar una cantidad (sustraendo) de otra (minuendo), es hallar una tercera cantidad llamada diferencia, que añadido al sustraendo reproduzca el minuendo. En la resta, se pueden suprimir los símbolos de agrupación: “( ), [ ], { }”; teniendo el cuidado de cambiar el signo de todos los términos que se encuentren dentro de ellos. Ejemplos: – (a + b) = – a – b – (– m + n) = m – n Al igual que la suma, se eliminan los signos de agrupación y posteriormente se suman o restan los términos semejantes. Ejemplos:
resta de monomios
1. 5abc - 3abc = (5-3)abc = 2abc 2. 3ab – 3bc = 3ab – 3bc No hay reducción porque no son términos semejantes. Para restar un polinomio de otro. Se restan los términos semejantes. Se deja indicada la resta de los términos desemejantes
Multiplicacion en las expresiones algebraicas:
Para la multiplicación algebraica se mantienen las mismas leyes que para la multiplicación aritmética, las cuales son:
Ley de signos: el resultado es negativo si la cantidad de factores negativos es impar, de lo contrario es positivo.
(+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = -
Ley de exponentes: el producto de dos o más potencias de la misma base es igual a la base elevada a la suma de las potencias.
(xm) (xn) = xm + n
Ley conmutativa: el orden de los factores no altera el producto
(x) (z) (y) = (y) (z) (x) = (z) (x) (y) = xyz
Pero en el álgebra se obedece también la ley de los coeficientes.
Ley de los coeficientes: el coeficiente del producto de dos o más expresiones algebraicas es igual al producto de los coeficientes de los factores.
(4x) (5y) = 4 · 5 · x · y = 20xy
Multiplicación de monomios: Se le llama multiplicación de monomios a la multiplicación de un solo término por otro término.
Reglas:
Se multiplica él termino del multiplicando por él termino del multiplicador.
Se suman los exponentes de las literales iguales.
Se escriben las literales diferentes en un solo término resultado.
Se coloca el signo de acuerdo con las reglas de los signos vistas anteriormente.
Cuando existen multiplicación más de dos monomios resulta sencillo multiplicar uno a uno los factores para obtener el resultado.
Ejemplos:
En el último ejemplo se multiplican primero los dos primeros factores entre si, sin tocar el resto, luego se multiplica este resultado por el tercer factor, por último se multiplicó este segundo resultado por el cuarto factor obteniéndose el resultado final.
Division en las expresiones algebraicas:
Para dividir monomios se resta los exponentes de las potencias de misma base siguiendo la ley de los exponentes
Ejemplo:
División de un polinomio por un monomio
Para dividir un polinomio entre un monomio basta con dividir cada uno de los términos del dividendo entre el término del divisor.
Ejemplo:
restando los exponentes de las potencias de la misma base se obtiene el resultado:
División de polinomios entre polinomios
La división algebraica se realiza de manera semejante a la numérica;
Si se tiene la división
1. Se ordenan de manera decreciente los términos de los polinomios, quedando la división:
2. Se obtiene el primer término del cociente dividiendo el primer término del dividendo (–2x2) por el primer término del divisor (x):
3. Se anota como cociente (-2x) y se multiplica por el divisor (x+4), se anotan los productos debajo del dividendo y se realiza la sustracción.
4. se vuelve a dividir el primer término que quedó en el dividendo (3x) por el primero del divisor (x) y se repite el proceso anterior.
Se ha obtenido cociente –2x + 3 y resto 0
Productos
se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores.
Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saberfactorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.
Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.
A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).
cuadrado de la suma de dos cantidades o binomio cuadrado:
a2 + 2ab + b2 = (a + b)2
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a2 + 2ab + b2 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)2
Nota:
Se recomienda volver al tema factorización para reforzar su comprensión.
Mas adelante lo podremos ver
Cociente notable:
Los cocientes notables son aquellos que resultan de divisiones exactas entre polinomios, es decir que el resto es igual a cero.
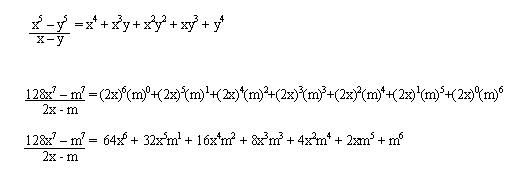
Forma general de un cociente notable
Factorizacion:
la factorización es una técnica que consiste en la descripción de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc.) en forma de producto. Existen distintos métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que reciben el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles.
El teorema fundamental de la aritmética cubre la factorización de números enteros, y para la factorización de polinomios, el teorema fundamental del álgebra. La factorización de números enteros muy grandes en producto de factores primos requiere de algoritmos sofisticados, el nivel de complejidad de tales algoritmos está a la base de la fiabilidad de algunos sistemas de criptografía asimétrica como el RSA.
potenciacion y radicacion en los numeros reales:
potenciacion:
La potenciación es una operación matemática entre dos términos denominados: base a y exponente n. Se escribe an y se lee usualmente como «a elevado a n» o «a elevado a la n»
Hay algunos números especiales, como el 2, al cuadrado o el 3, que le corresponde al cubo. Nótese que en el caso de la potenciación la base y el exponente pueden pertenecer a conjuntos diferentes, en un anillo totalmente general la base será un elemento del anillo pero el exponente será un número natural que no tiene porqué pertenecer al anillo. En un cuerpo el exponente puede ser un número entero.
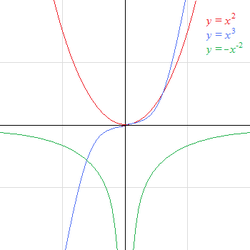
radicacion:
La radicación es la operación inversa a la potenciación. Y consiste en que dados dos números, llamados radicando eíndice, hallar un tercero, llamado raíz, tal que, elevado alíndice, sea igual al radicando.

En la raíz cuadrada el índice es 2, aunque en este caso se omite. Consistiría en hallar un número conocido su cuadrado.

La raíz cuadrada de un número, a, es exacta cuando encontramos un número, b, que elevado al cuadrado es igual al radicando: b2 = a.

Raíz cuadrada exacta:
La raíz cuadrada exacta tiene de resto 0.
Radicando = (Raíz exacta)2

Cuadrados perfectos:
Son los números que poseen raíces cuadradas exactas.
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, ...
Raíz cuadrada entera:
Si un número no es cuadrado perfecto su raíz es entera.
Radicando = (Raíz entera)2 + Resto

Algoritmo de la raíz cuadrada:

1Si el radicando tiene más de dos cifras, separamos las cifras en grupos de dos empezando por la derecha.

Geometria:
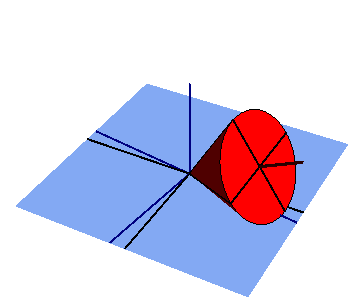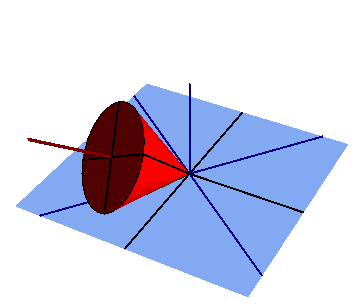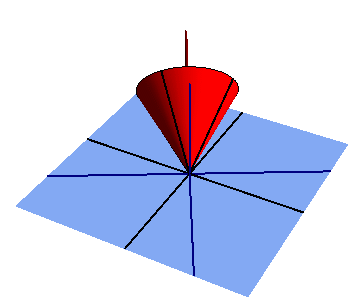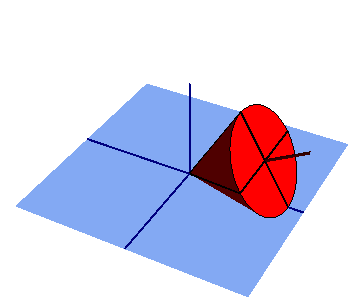
Rotación:
significa girar alrededor de un centro:
La distancia del centro a cualquier punto de la figura es la misma.
Cada punto sigue un círculo alrededor del centro.
Puedes girar objetos (punto a punto) con cualquier ángulo, alrededor de cualquierpunto central.
Traslación:
Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualquier punto P y Q se cumple la siguiente identidad entre distancias:
Más aún se cumple que:
Notas:
La figura trasladada es idéntica a la figura inicial.
La figura trasladada conserva la orientación que la figura original.
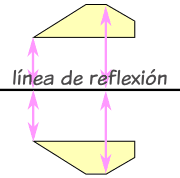
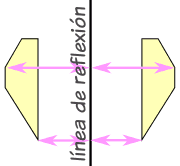
Reflexion:
La línea central se llama línea de reflexión .
. y no importa en qué dirección vaya el reflejo, la imagen reflejada siempre tiene el mismo tamaño, pero en la otra dirección:

Una reflexión es una transformación geométrica. En una reflexión, un objeto geométrico “se mueve de un tirón” a través de una recta. La recta a través de la cual se refleja un objeto se llama la recta de reflexión o el eje de la reflexión.
ESTADISTICA:
variable cualitativa:
significado
Son aquellas variables cuyos valores son un conjunto de cualidades no numéricas a las que se llama categorías o modalidades.
clasificacion de una variable cualitativa:
Escala nominal: No se puede definir un orden natural entre sus categorías. (Ejemplo: la raza, el color del pelo, o la religión)
Escala ordinal: Se pueden establecer relaciones de orden entre las categorías. (Ejemplo: el rango militar, la clase social o el nivel de estudios)
Por intervalos: Pueden tratarse como ordinales y se pueden calcular distancias numéricas entre dos niveles. (Ejemplo: El número de años de educación recibidos (0, 1, 2, ...) es una variable cuantitativa que puede ser agrupada por intervalos)
Tabla de contingencia:
En estadística las tablas de contingencia se emplean para registrar y analizar la asociación entre dos o más variables, habitualmente de naturaleza cualitativa(nominales u ordinales)
Supónga que se dispone de dos variables, la primera el genero(hombre o mujer) y la segunda recoge si el individuo es zurdo o diestro. Se ha observado esta pareja de variables en una muestra aleatoria de 100 individuos. Se puede emplear una tabla de contingencia para expresar la relación entre estas dos variables:
Diestro Zurdo TOTAL
Hombre 43 9 52
Mujer 44 4 48
TOTAL 87 13 100
Las cifras en la columna de la derecha y en la fila inferior reciben el nombre de frecuencias marginales y la cifra situada en la esquina inferior derecha es el gran total.
La tabla nos permite ver de un vistazo que la proporción de hombres diestros es aproximadamente igual a la proporción de mujeres diestras. Sin embargo, ambas proporciones no son idénticas y la significación estadística de la diferencia entre ellas puede ser evaluada con la prueba χ² de Pearson, supuesto que las cifras de la tabla son una muestra aleatoria de una población. Si la proporción de individuos en cada columna varía entre las diversas filas y viceversa, se dice que existeasociación entre las dos variables. Si no existe asociación se dice que ambas variables son independientes.
TABLAS MARGINALES: Una tabla marginal es una tabla cruzada, en el cual se muestran frecuencias relativas con relación al total de cada fila o columna. Por ejemplo para la variable deporte preferido, la tabla marginal se construye hallando el cociente entre cada frecuencia y el total correspondiente a la columna; en estas tablas se elimina la columna de los totales, así:
Caracterizacion de una variable cuantitativa:
la caracterización de variables cuantitativas se debe realizar teniendo en cuenta la forma en la cual se van a presentar los datos. Para esto, se tienen en cuenta dos criterios:
* Si los datos están agrupados. * Si los datos no están agrupados.
Datos Agrupados
Cuando los datos obtenidos a partir de una variable cualitativa se van a presentar en forma agrupada se utilizan las siguientes herramientas para su caracterización.
DIAGRAMA DE TALLOS Y HOJAS :
Es la primera representación gráfica en la que se clasificacn los datos de acuerdo con la expresión decimal de cada uno de ellos. El tallo corresponde a la primera o primeras cifras del dato y en la mayoría de los casos la hoja corresponde a la última cifra del dato.
TABLAS DE DISTRIBUCION DE FRECUENCIAS:
Una tabla de distribución de frecuencias para variables cuantitativas está formada por:
– Intrevalos de clase – Frecuencia del Intervalo – Frecuandia relativa – Frecuencia Acumulada – Frecuencia relativa acumulada – marca de clase
HISTOGRAMAS :
Un histograma es la representación gráfica de una variable cuantitativa en la cual cada rectángulo representa una frecuencia.
POLIGONO DE FRECUENCIA:
Un polígono de frecuancias es un diagrama formado al asignar a cada marca de clase la frecuencia correspondiente a ese intervalo.
OJIBA: La ojiba es un grafico de líneas cuyos valores en el eje y son las frecuencias acumuladas.
Grafica de puntos:
Un diagrama de puntos es una gráfica utilizada para ilustrar un número reducido de datos, la cual permite identificar con facilidad dos características:
1. La localización de los datos.
2. La dispersión o variabilidad de los datos.
Este diagrama muestra cada uno de los elementos de un conjunto de datos numéricos por encima de una recta numérica (eje horizontal), facilita la ubicación de los espacios vacíos y los agrupamientos en un conjunto de datos, así como la manera en que estos datos se distribuyen a los largo del eje horizontal.

Gracias y les deseo suerte.



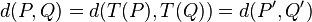
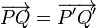
Comentarios